線形モデルを簡単にわかりやすく！ -データに直線を引いて、傾向を捉えるときの注意点-

線形モデルとは

今日のテーマは「線形モデル」です。多くの人が聞き慣れている「線形モデル」という言葉ですが、これについて今回はお話ししたいと思います。線形モデルは、他に「回帰モデル」という人もいますし、「線形回帰モデル」ということもあります。この辺の区別は、本来正確を期すべきですが、今回はここは気にしないで「線形モデル」を理解してもらうことに主眼を置きます。
線形モデルというのは、非常に単純なモデルです。下の図を見てください。データの点々によく当てはまる「線」を引いています。これはエクセルでも、統計ソフトでもなんでもできます。こうすると、実際にデータの傾向が見える化され、データから情報を引き出しやすくなります。今回は、この線形モデルの基本的なこと・それから注意点についてお話をします。少し統計的な言及を行いますが、できる限り直感的に説明をします。

f:id:tomoshige_n:20140117022414p:plain

用いるデータ

線形モデルを説明するために、今回は「データ」を用いることにします。ここでは、仮想のデータですが「農地に投入した肥料（変数名：fert）」と「収穫量（変数名：harvast）」の関係性を考えていきます。ここで、回帰モデルを考える時は「説明したい変数, 説明される変数, 予測したい変数」のことを「目的変数」と呼びます。つまり「収穫量」が目的変数です。一方で、「予測したい変数」を「説明する変数」今回であれば「農地に投入する肥料の量」を説明変数と呼びます。これは覚えてください。以下がデータです。ここで、最後の列の変数名「harvest_log」は「収穫量を対数変換」したものです。

> head(dat) #データの最初の行だけ見ます
  fert   harvest harvest_log
1   15  68.47501    4.226469
2   12  32.80894    3.490701
3   27 134.21358    4.899432
4    2 149.71490    5.008733
5   23  34.95415    3.554037
6   24 183.13655    5.210232

やりたいこと

さて、行いたいことは「肥料の量」と「収穫量」には「どのような関係性」があるのかを確かめるということだとします。すると、真っ先に思いつくのは、横軸に、「肥料の量」をとり、縦軸に「収穫量」を取るようなことです。実際に図にしてみると、次のようになります。

f:id:tomoshige_n:20140814002040p:plain

この図から、読み取れることとしては、「肥料の量」が多くなるに連れて、「収穫量」は「指数的に」増えていることが見て取れます。つまり、式として書けば...

$収穫量 = \exp\{（切片）+ （肥料の量）＋（観測誤差）\}$

となっています。

線形モデルとは

さて、ここで、「線形モデル」の「線形」の意味を考えておくと、「線形」というのは、「目的変数」と「説明変数」の関係性が線形ですということを意味しています。これはどういうことかというと、目的変数は次のように表されますという仮定を置いています。言葉にすれば次のようになります。

$目的変数= 切片 + 説明変数1 \times 回帰係数1 + ... + 説明変数p \times 回帰係数p + 観測誤差$

数式では...（正確には、今回のケースでYやXはベクトルです）

$Y= \beta_{0} + X_{1}\beta_{1} + \cdots + X_{p}\beta_{p} + \varepsilon$

これを見ればわかっていただけるように「線形モデル」の「線形」の意味は「目的変数」と「説明変数」の関係性の間に「非線形な関係」が紛れ込んではいけないのです。例えば「exp」とか「log」とかの関係性が入ると、途端に仮定が崩れて「線形モデル」を使うことはできません。ただし、モデルへ取り込む方法はありますが、それは次のエントリーで書くことにします。ただ、YとXの関係が"Y=exp(X)*b+e"だと推測されるのに、"Y = Xb+e"とモデルを仮定してはいけませんという話です。

そのため、線形モデルを用いる際には「変数間」の関係性に注意する必要があります。想い出してほしいのですが「相関」についてのエントリー「相関係数」ってなんですか？ -意味と利点と欠点をわかりやすく- - Data Science by R and Pythonでも説明しましたが「説明変数」と「目的変数」の間の「線形性」に注意を払う必要があります。これを気にしないで「えいや！」ってやってしまうとろくな結果がでません。

実際に、線形回帰モデルの「回帰係数」上でいえば、 $\beta_{j}$ にあたる部分の値というのは、目的変数Yと $X_{j}$ の相関係数の関数なので、この値に依存しています。この点には注意してください。

今回のケース

そのため、今回のケースに線形回帰モデルを当てはめてはいけません。実際に当てはめてみると、次のような結果が得られます。図で確認しましょう。

f:id:tomoshige_n:20140814004447p:plain

これを見ていただくとわかるように、図から「外れている」ものがたくさんあります。特に「肥料の量」が大きくなると、「外れるのが大きく」なることが見て取れます。実は、このようなデータをそのまま扱う手段というのがあります。それは「Gamma分布を事前分布に仮定する」という方法で、一般化線形モデルの枠組みで話すことができます。でも、今回は「線形モデル」で扱うことに主眼があるので、このような場合の対処法を考えていきましょう。

指数的な関係性・対数的な関係性。

さて、目的変数と説明変数の間に、指数的な関係性があることがわかっています。指数的な関係というのは、具体的な例をだせば「xが1から2に増えると、Yはexp(1)=2.7 からexp(2)=7.4に増える」という関係性があるような状態です。今回のデータでは次のような関係です。

$収穫量 = \exp\{（切片）+ （肥料の量）\times （回帰係数）＋（観測誤差）\}$

そんなときに効果的な対処の方法があります。それは両辺の「対数」を取るということです。両辺の対数を取ると、式は次のように変形されます。

$\log(収穫量) = （切片）+ （肥料の量）\times （回帰係数）＋（観測誤差）$

これを見ていただくとわかる通り、これは、目的変数をlog(収穫量) とすれば、目的変数は「肥料の量」の線形式で表されるということを意味します。つまり、こうすれば「線形回帰」できるのです。実際に横軸は（肥料の量）で、縦軸をlog(収穫量) として図を書いてみます。すると、、、

f:id:tomoshige_n:20140814005626p:plain

このようなデータを得ることができました。このデータを見ていただくとわかるように、目的変数と説明変数の間には確かに「線形の関係」が存在することがわかります。これに回帰直線を引いたら次のような図が得られます。

f:id:tomoshige_n:20140814005759p:plain

奇麗に回帰ができているようにみえますね。

ネタばらし。

今回の架空のデータの生成方法についてここで書いておきますと、実は、モデルの片々を対数をとったら線形モデルになるようにデータを設計していました。コマンドは下に書いています。

$\log(収穫量) = 4+ （肥料の量）\times 0.03＋（正規分布：平均0, 分散1/2に従う乱数）$

このようにしているため、きちんとlogを取らないと正確な結果は得られません。実際に対数をとったものと、取ってないものを比較してみると以下のようになります。もちろんスケール変更しているため直接比較は難しいですが、対数を取ったケースを見ていただくと、切片を3.97532（本来は4）、fertの回帰係数の推定値0.02925（真の値は0.03）とうまく推定できていることがわかります。図を確認してから回帰する理由が何となくわかっていただけましたか？

#対数を取っていない場合
> glm(harvest ~ fert, data=dat)

Call:  glm(formula = harvest ~ fert, data = dat)

Coefficients:
(Intercept)         fert  
     37.935        3.889  

Degrees of Freedom: 99 Total (i.e. Null);  98 Residual
Null Deviance:	    874200 
Residual Deviance: 615900 	AIC: 1162

#対数を取った場合
> glm(harvest_log ~ fert, data=dat)

Call:  glm(formula = harvest_log ~ fert, data = dat)

Coefficients:
(Intercept)         fert  
    3.97532      0.02925  

Degrees of Freedom: 99 Total (i.e. Null);  98 Residual
Null Deviance:	    39.73 
Residual Deviance: 25.12 	AIC: 151.6

線形回帰モデルにおける重要な仮定

さて、線形回帰モデルにおけるもう1つ重要な仮定があります。これは、普通に「最小自乗法」という当てはめで線形回帰モデルが成り立ってるんだ！と思っていると、全く気づきませんが、知っておいてほしいことです。理由を説明し始めると、かなり長くなるので今回は紹介にとどめますが「等分散性」の仮定というものがあります。これは、なにかというと次の図を見てください。

f:id:tomoshige_n:20140814011725g:plain

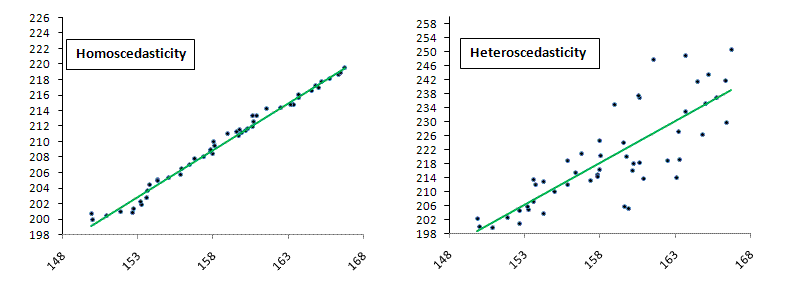
左側と右側の違いわかりますか？左側の方はX軸の値が大きくなっても、データのちらばりは変わりません。しかしながら、右の図を見ていただくと、X軸の値が大きくなるに連れて、データの散らばりが大きくなっています。

このような場合、左側は「等分散」であり、右側は「不均一分散」であると言います。そして、線形モデルには、データが「等分散である」という仮定が置かれていますので、目的変数と説明変数が「不均一分散」な関係性を持っている場合には「線形回帰モデル」は使うことができないというのが覚えておいて欲しいことです。

このような場合には、先ほど少しでてきた「一般化線形モデル」を用いたり、この他「線形混合モデル」、または「一般化線形混合モデル」さらには「一般化加法モデル」を用いたりします。このように、様々な手法を用いてこの問題を解消することができますが、線形モデルのみの枠組みでこの問題を取り扱うのはいささか難しいと言えます。

まとめ

さて、今回は「線形回帰モデル」について説明をしました。少し統計的な話も入ってきて、難しかった人もいるかもしれませんが、データ解析の基本が「図を書いて」「変数同士の関係性」をチェックするというところに変わりはありません。統計やデータの分析を行う際には、「図を書く」ことをとにかく大切にしてほしいと思います。
それから、線形回帰モデルというのは、今私たちが統計の世界で用いている手法の「基礎」になっているモデルです。実際、このモデルを拡張することで、様々なモデルが歴史的に作られてきました。なので、統計をやるにあたって「線形回帰モデル」をきちんと勉強して、使えるようになることは、ある意味その他の分野・手法を勉強・研究する際の大きな助けになります。是非、統計を始めよう！解析を始めようと思っている方は、「線形回帰モデル」からはじめてください！

お知らせ：データフェスト

データフェストを開催しますと以前ブログで書きましたが、開催の予定日程が変更になっていますのでご注意いただければと思います。会場の都合などで変更になりました、、、申し訳ないです。
【予告】データフェストを開催します！（仮） - Data Science by R and Python

コマンド

#wd
setwd("~/Desktop/blog/lm")

#library
library(ggplot2)
set.seed(100)


############
##dataの作成#
############

#肥料
fert=floor(runif(100,0,50))
#対数を取った収穫量
harvest_log=4+fert*0.03+rnorm(length(K),0,0.5)
#収穫量の観測値
harvest=exp(harvest_log)

#data
dat=data.frame(fert,harvest,harvest_log)

#plot by ggplot2

#lm not good
ggplot(data=dat,aes(x=fert,y=harvest))+geom_point()+xlab("amount of fertilizer")+ylab("harvest")

#lm not good
ggplot(data=dat,aes(x=fert,y=harvest))+geom_point()+geom_smooth(method="lm")+xlab("amount of fertilizer")+ylab("harvest")

#lm good
ggplot(data=dat,aes(x=fert,y=harvest_log))+geom_point()+xlab("amount of fertilizer")+ylab("log harvest")

#lm good
ggplot(data=dat,aes(x=fert,y=harvest_log))+geom_point()+geom_smooth(method="lm")+xlab("amount of fertilizer")+ylab("log harvest")

#glm result not good
glm(harvest ~ fert, data=dat)

#glm result good
glm(harvest_log ~ fert, data=dat)