「相関係数」ってなんですか? -意味と利点と欠点をわかりやすく-
「相関」って何.
統計学を学んだことがあれば、誰もが一度は聞いたことがある「相関」という言葉。最近では、高校でも扱われる概念になったようですが、「相関」っていったい何でしょうか?教科書(という名のWikipedia)にはこういう風に書かれています。
相関係数(そうかんけいすう、英: correlation coefficient)とは、2 つの確率変数の間の相関(類似性の度合い)を示す統計学的指標である。原則、単位は無く、−1 から 1 の間の実数値をとり、1 に近いときは2 つの確率変数には正の相関があるといい、−1 に近ければ負の相関があるという。0 に近いときはもとの確率変数の相関は弱い。因みに 1 もしくは −1 となる場合は 2 つの確率変数は線形従属の関係にある。
ここでは、相関ではなく、相関係数という言葉を用いていますね。「相関」というのは、2つ以上のもとがあるときに、それらが「どれぐらい類似しているか」という「類似度」を意味します。そして、相関係数とは、「類似度」の強さを「−1から1」までの範囲を取る数字として表現したものです。
この「相関」という考え方は一般的にもよく使われます。データ解析するときは、必ず「変数」と「変数」の「相関」をチェックします。例えば、「がんのリスク」と「BMI」の関係を見たいなんていうときは、まずは「相関」を見るわけです。この相関係数は、データを眺めるという解析の基本においては強力な力を持っています。しかしながら、この「相関」には実はいろいろと落とし穴があります。それを見ていきましょう。
僕らがよく利用する相関
私たちがよく利用する「相関」は「ピアソンの積率相関係数」というものです。以下では、「ピアソンの積率相関係数」を「相関係数」と呼んで議論を進めます。さて、この「相関係数」は先ほども説明した通り「変数」と「変数」の類似度を測るための「-1から1」までの値をとる指標ですが、どんなものが高い相関を持つのかは、次の図を見ていただければよくわかります。
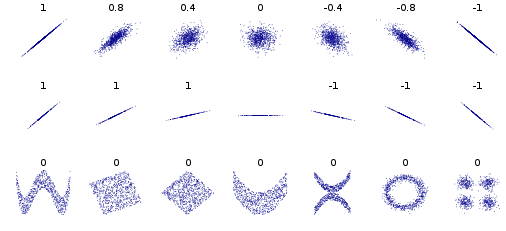
さて、お気づきになりましたか?相関係数というのは、実は「変数」と「変数」の関係が「直線」の場合にのみ1をとります。実はここがとても大事なところです。先ほどの「がんのリスク」と「BMI」の関係性を見たいときに、指標として「相関係数」を用いても実は関連性は発見されません(相関係数は0に非常に近い値になります)。それは、この2つの変数の関係性は次のようになっているからです。

出典 : http://epi.ncc.go.jp/can_prev/evaluation/2830.html
つまり、「ピアソン相関」の考え方は「線形関係」を発見するものであり、残念ながら「非線形」な関係には効果を持ちません。例えば、「がんのリスク」と「BMI」の関係性は「2次曲線」っぽいですよね。つまり、この2つの間には「相関」はないとなってしまいます。しかしながら、私たちは気づいている通り、この2つの間に「関係性」は存在します。この議論の続きは後の章で行います。まずは、相関係数についてもう少し深く議論をしておきます。
相関係数の定義式ともう少し深い議論へ(必要ない方は読み飛ばしてください)
もう少し詳しい議論をするために、「相関係数」の定義を書いておきます。ここで、議論を深めるためには、確率変数とその実現値という考え方を導入する必要があります。議論が複雑なので、難しい方は読み飛ばしてください。そして、ここからは日本語のwikipediaでは正確な議論が展開されないので、英語のwikipediaを参考にして進めていきます。
下にwikipediaの引用を記しました。さて、ここで、「Pearson's correlation coefficient when applied to a population」が母集団の相関係数です。一方で、「Pearson's correlation coefficient when applied to a sample」が標本に対する相関係数です。つまり、母集団の相関を、標本を用いて推定した式が「標本に対する相関係数」です。この推定した値が「私たちが普段接する」相関係数に対応します。
すると、ここで気になることが出てきます。それは、「母集団に対する相関係数」と「標本に対する相関係数」が一致するのかという疑問です。実際、推定値が母集団に対する相関係数を「近似」しないのであれば、標本に対する相関係数を見ても、背後に潜む真の相関はわかりません(実際、背後に潜む相関を見抜くには、以下の議論以外にも考慮する必要のある事柄があります)。
そこで、標本から推定される相関係数が母集団の相関係数をどの程度近似するのかを考えなくてはなりません。つまり標本から得られた「相関係数の推定値」を評価する必要があります。そのときに、用いる考え方は「不偏性」「有効性」「一致性」の3つです。また、これらの性質を確認するためには、「標本」に分布の仮定が必要です。分布の仮定として有名なのは「正規分布」なので、まず正規分布を仮定した場合を考えましょう。
正規分布を確率変数XとYに仮定する場合
このとき、標本から推定される相関係数の推定値は、母集団の相関係数のMLE(最尤推定量)となり、漸近的に「不偏性」「有効性」「一致性」の3つを満たすことがわかります。つまり、標本数がある程度大きければ、推定量として良い性質を持っていることが理解できます。
正規分布ではない、確率変数X,Yを仮定する場合
このとき、標本から推定される相関係数の推定値は、「不偏推定量」かつ「一致推定量」ですが、残念ながら「有効推定量」ではありません。つまり、不偏推定量のなかで、これよりもばらつきの小さい(平均自乗誤差を小さくする)推定量が存在するということになります。
さらに相関係数の弱点 -robust性から-
さらに相関係数には、弱点があります。それは「ロバスト性」がないということです。これはつまり「はずれ値」に影響を受けやすいということです。例えば母集団の分布(データの標本を見て)「裾が重い分布」や「ゼロインフレートな分布」に対しては、相関係数は統計的な解釈をする上で意味のあるとは言いがたいということになります。この点は忘れやすいので注意してください。
また、実際に「相関が0かそうではないか」を仮説検定・区間推定をする場合があります。このときにFisher Transformを用いて計算をすることがありますが、これにも注意が必要です。この変換を行う場合にはいつも「漸近的に変数の同時分布が2変量正規分布に従う」という仮定が置かれます。しかしながら、これを満たさない分布(標本が十分に大きくない場合も含む)にたいして使うと、間違った結果を招きかねません。このような場合には「ノンパラメトリック」な手法で、ブートストラップ法などをもちいるのが良いでしょう。
相関係数への誤解(飛ばした人は、ここから読んでください!)
続けて、「相関」についての考え方の間違いをいくつかご紹介しましょう。
相関係数は順序尺度である。
よく、相関係数が「ケース1では0.8」と「ケース2では0.4」のような表現がある場合に「よって、ケース1の方がケース2より、2倍相関が強い」と言っている人がいますが、これは間違いです。相関には「より大きい」と「より小さい」の表現しかありません。その大きさについて議論をすることはできないことに注意が必要です。
相関と因果の関係性に注意せよ!
「相関関係」があるということを聞くと、あたかも「因果関係」があるように捉えてしまう方がいらっしゃいます。しかしながら、これにも注意が必要です。ここで、正しく宣言しておくと「相関関係は、因果関係と同じではなく、相関関係は因果関係の必要条件の1つである」というのが正しいです。つまり、「因果関係」を説明するには「相関関係」がないといけないが、「相関関係」を説明するのに、「因果関係が必要」とは言ってないのです。実は、相関関係が生じる原因はいくつかに分類されます。相関がある場合には、可能性として次のことが考えられます。
- BがAを発生させる
- AがBを発生させる
- AとBは共にCが発生させている(疑似相関)
- AとBには関係がないが...偶然相関が生じた
- AとBが互いに原因と結果の関係にある(ポジティブフィードバック)
ここまでで、わかりましたか?相関は因果関係ではないのです。
因果関係の立証
因果関係を立証するためには、次のようなことを示す必要があります。偶然の相関ではない、AとBが互いに原因と結果の関係ではないとしましょう。このとき、次の3つが成立しなければ、因果関係であると結論づけることはできません。
XがYの原因であると結論づけられるとき
1.XはYに先行して発生している
2.YはXが起きないときに発生しない
3.YはXが起きたら、必ず発生する(緩和されることもある)
が成立している必要がある。
これが成り立たないとき、何か共通の原因Cによって影響を受けていると考えて、因果モデルの構築を変更するのが望ましいといえる。
因果関係の判定
因果関係の判定についても少し述べておきます。因果関係を判定するためには、「反事実的依存関係」と調べる必要があります。これは何かというと、太った男性がいる場合に、ここ2ヶ月「暴飲暴食」をしたからと結論づけるには、時を2ヶ月巻き戻して「同じ状態」で「暴飲暴食」しない場合を確かめないといけないということです。しかしながら、これは現実的に不可能ですよね。これは「因果的推論の根本問題」と呼ばれています。このような問題を補正するために、先日資料をアップした「傾向スコア」の考え方が用いられたりするのですが。
非線形な関係性を見つけるには?
最後に、非線形な関係性ーさきほどの「がんのリスク」vs「BMI」のような相関を発見する方法を紹介します。これには、いろいろな手法が提案されている。詳しくは別の機会に書くことにするが、以下のようなものが存在しています。上2つは聞いたことがある人もいらっしゃるのでは?
- スピアマンの順位相関係数 Spearman's rank correlation coefficient - Wikipedia, the free encyclopedia
- ケンドールの順位相関係数ケンドールの順位相関係数 - Wikipedia
これ以外も、この後に紹介する予定の「相互情報量」に基づく手法である「Maximum Information Coefficient」があります。この方法は「21世紀のデータから関係性を見つけ出す手法」としてサイエンス誌にも掲載された手法です。この他の手法としては再生核カーネルヒルベルト空間(RKHS)に基づくHSICという方法もあります。これらも、夏の間に紹介しようと思っています。
終わりに
いかがでしたか?相関1つとっても実は、いろいろと議論をする必要があることがあります。統計を武器としてを使うときに行ってはいけないことは「数学的」な議論を抜きに手法を振り回すことだと思います。僕も、まだ人のことを言えないんですけど、こういうことに意識が向かないけど、統計を使う人の助けに少しでもなりたいと思っています。データサイエンティストの大事な役割ってこういうところにあるのかもしれません。連続ブログも、6日目に突入...
注意
今回は、最初日本語のwikipediaや統計の教科書を参考にしましたが、あまり良い議論ができていないため「英語のwikipedia」とStatistical Inferenceという本を参考にして書いています。推定量の性質など。Inductive Statistics
このあとやりたいこととか、いろいろ(毎回更新していく予定)
ブログネタ書きだめ場所
R stan & 階層ベイズ
R Tips
- data.frame を ggplot2 用に加工する - joker8phoenix's diary
- ggplo2
- shiny
- dplyr
空間統計学
- Spatial Analysis
Machine Learning
- Random Forest
- Boosting
- SVM, RVM
- Graphical Modeling
- Neural Network
予定...
- 8月27日 ~ 8月29日は欠測データ周辺についてブログを書きます(星野先生がうちの大学で欠測データ補完についての集中講義をするため)。
