時間ができたので一般化線形モデル(ロジスティック回帰)のコードを書いてみた
ロジスティック回帰
ロジスティック回帰モデルといえば、一般化線形モデルの代表格で、統計を少しでも勉強している人は知っている・聞いたことのある手法だと思います。今回は、そのロジスティック回帰を実際にRでプログラムするということをやってみます。ちなみに、Rはもともとglmという関数が入っていて、そこでfamily="binomial"とすれば、それで終わりなんですけど、まぁつくってみる・手を動かすのも大事なのでやってみました。
注)逸脱度の計算と、尤度計算はまだしていませんがちゃんとしないと...
一般化線形モデルの枠組みについて
一般化線形モデルの枠組みについては、Dobson(2002)がわかりやすいです。日本語も出ていて、「一般化線形モデル入門」でググってもらえばすぐにでます。
プログラムの内容
データはDobson(2002)のものをサンプルとして使用します。xは密室内に充満するガスの濃度、nはガスを注入した密室内にいる虫の数、yはそのうちガスの注入で死んだ虫の数です。このとき、死んだ虫の数yは2項分布に従うと考えることができて、これをガスの濃度で説明するモデルを考えます。これは、一般化線形モデルに置けるロジスティック回帰モデルです。ロジスティック回帰モデルというと、目的変数が「0か1」と考える方が多くいらっしゃいますが、大きな枠組みとしては、目的変数の分布に2項分布を仮定することです。つまり、正確な記述としては、
というものになります。ロジスティック回帰の名前の由来というのは、以下の式の左辺を「ロジット変換」と呼ぶからです。それから、この式の左辺を「リンク関数」と呼びます。そして、この形は「正準リンク」と呼ばれていて、このリンク関数を用いると嬉しい性質がいくつかありますが、今回は言及を避けましょう。ただ、皆さんが用いているロジスティック回帰モデルには、色々と背景があるんだなということを知っておいていただければ。
Rで書いた関数
#sample data
x=c(1.69,1.72,1.75,1.78,1.81,1.83,1.86,1.88)
n=c(59,60,62,56,63,59,62,60)
y=c(6,13,18,28,50,53,58,59)
#GLM for binomial
p_calc=function(x,b){
exp=exp(x%*%b)
pp=exp/(1+exp)
return(pp)
}
glm_bin=function(x,n,y,eps=1e-08,fig=T){
#data frame
#if(is.vector(x)==TRUE){
x=cbind(rep(1,length(x)),x) #intercept
#}else{
# x=cbind(rep(1,nrow(x)),x) #intercept
#}
#start value
beta=rep(0,ncol(x)) #regression coef
pp=p_calc(x,beta) #probability
mu=n*pp #expectation of y
W = diag(as.numeric(n*pp*(1-pp))) #inverse of var(y)
z = x%*%beta + solve(W)%*%(y-mu)
#calc
for(i in 1:25){
stop = i #save i
bbsave=beta
beta = solve(t(x)%*%W%*%x)%*%t(x)%*%W%*%z
pp=p_calc(x,beta)
mu=n*pp
W = diag(as.numeric(n*pp*(1-pp)))
z = x%*%beta + solve(W)%*%(y-mu)
sqdf=sum(t(bbsave-beta)%*%(bbsave-beta))
if(sqdf < eps){
break;
}
}
dev=2*(sum(y*log(y/(mu))+(n-y)*log(n-y)-(n-y)*log(n-mu)))
lp=x%*%beta
#names(beta)=c("intercept","X1")
ans=list(iter=i,beta=beta,prob=pp,linear.predictor=lp,y.fitted=mu,deviance=dev)
return(ans)
}
#plot
#library
library(ggplot2)
#dataframe
dat = data.frame(gas=x,rate=y/n)
gas=seq(min(x)-0.1,max(x)+0.1,0.001)
sam=cbind(rep(1,length(gas)),gas)
pline=sam%*%rr$beta
pline=exp(pline)/(1+exp(pline))
dat2 = data.frame(gas,pline)
#plot
(fig=ggplot(data=dat,aes(x=gas,y=rate))+geom_point()+geom_line(data=dat2,aes(x=gas,y=pline)))
結果の確認
#自作のプログラムの結果
$iter
[1] 6
$beta
[,1]
-60.81594
x 34.40013
$prob
[,1]
[1,] 0.0641806
[2,] 0.1614176
[3,] 0.3507569
[4,] 0.6025951
[5,] 0.8097357
[6,] 0.8943813
[7,] 0.9596238
[8,] 0.9792919
$linear.predictor
[,1]
[1,] -2.6797215
[2,] -1.6477177
[3,] -0.6157139
[4,] 0.4162900
[5,] 1.4482938
[6,] 2.1362964
[7,] 3.1683003
[8,] 3.8563028
$y.fitted
[,1]
[1,] 3.786655
[2,] 9.685059
[3,] 21.746927
[4,] 33.745328
[5,] 51.013350
[6,] 52.768495
[7,] 59.496674
[8,] 58.757512
$deviance
[1] 1551.011
#Rに元々入っているものの結果
> rr2=glm(cbind(y,n-y)~x,data=dd,family="binomial",epsilon=1e-08)
> rr2
Call: glm(formula = cbind(y, n - y) ~ x, family = "binomial", data = dd,
epsilon = 1e-08)
Coefficients:
(Intercept) x
-60.82 34.40
Degrees of Freedom: 7 Total (i.e. Null); 6 Residual
Null Deviance: 284.2
Residual Deviance: 9.699 AIC: 39.9
Coefficientが一致しているので問題ない。
ただ、iterationは通常のglm関数の方が少ないので、なんかもう少し関数考えた方がいいかもしれない...wood(2006)のGAMで使う方法を用いる方がいいのかねぇ。。。
Shiny -Rでつくるウェブアプリケーション!-
shinyでウェブアプリケーションを作成する
Rでは、"shiny"というライブラリを使うことで、ウェブアプリケーションを作成することができます。僕も、最近知って今日初めて少しだけ勉強したので、ここに書いてみます。まだ、少ししか見ていないのですが、結構可能性のあるライブラリだなと思っています。最後の参考という項目にいろいろ書いているので、是非見てください!
ウェブアプリケーションの構成
shinyで作成するアプリケーションは「ui.R」と「server.R」の2つから構成されます。「ui.R」には、ユーザーインターフェースの情報を下記、「server.R」には、サーバーがどのように動作してほしいのかを記述します。
さて、ui.Rは、shinyUI関数からつくります。このshinyUIの中身には、「headerPanel」「sidebarPanel」「mainPanel」の3つの関数から構成します。それぞれが、ウェブ作成で言うところの、ヘッダー、サイドバー、メインコンテンツに対応しています。ここにそれぞれの表示したい部品を設定するということになります。※)ちなみに、いろんな書き方があるようです。
以下、サンプルコードです。
#ui.R
library(shiny)
#define UI
shinyUI(
pageWithSidebar(
#header
headerPanel("Hello Shiny"),
#sidebar
sidebarPanel(
sliderInput(
"obs",
"Number of observations:",
min=0,
max=1000,
value=500
)
),
#main page
mainPanel(
plotOutput("distPlot")
)
)
)サーバー側はこんな感じで。
#server.R
library(shiny)
#define server logic required to plot various variables against mpg
shinyServer(function(input, output){
output$distPlot <- renderPlot(function(){
dist <- rnorm(input$obs)
hist(dist)
})
})
書き終わったら、何らかのフォルダーに保存して、ターミナルから以下のコマンドを打てば、動き始めます。それから、ブラウザーでそのURLを開けば終わりです。
R -e "shiny::runApp('ディレクトリ')"
まとめ
なんか、本当に勉強はじめで、今回のはR上級ハンドブックを参考に書かせていただきました。今、下記のページで勉強中ですのでレベルアップしたら、また書きます。
僕が、統計学を始めた理由 -興味の中心にはいつも「ヒト」がいるみたいです-
今日は雑記
今日まで何日か、Rの使い方を書いてきたので、今日は「僕が、どうして統計学」に飛び込んだかという話を書いてみようと思います。昨日から「Sunny Brain, Rainy Brain」という本を読んでいる影響です。ちなみにこの本には「ポジティブ」と「ネガティブ」な脳に関係する様々なことが書かれています。オススメです。ただ、この本を読んでいて、なんで自分が統計学を学び始めたのか、今どうしてこんな風に考えるのか気になってきました。なので、書き残しておこうと思います(いつか見返して、ここ違う!とか,いろいろ思うこともあると思うので)。
はじまりは大学1年生の夏
僕は、大学に入った理由は「数学者」を目指すためでした。高校では、ずっと数学が好きで勉強してきました。成績もそこそこ良かったけど、ただ○○で何位とかそんな素晴らしいレベルではありませんでした。そして、今の大学に入学して、大学1年生の夏にさしかかった頃、僕はなんというか「このままでいいのか」と思いました。というのは、「大学で勉強する意味」がわからなくなりました。というのは、今学んでいることが、何の役に立つのか「微塵も」みえなくなった。「わからないこと」があると、それを「理解しよう」とするんだけど、どうも気持ちは「別にわからなくてもいいよ、大好きなゲームしたら?」って言ってました。
そんな自分の逃げ道は、「ビジネスコンテスト」を開催している団体です。人にあうことは好きでしたし、話すのも好きでした。それから、本当にいい先輩ばかりだったし、同期も愉快な人ばかりだったと思います。別に仕事が楽しいわけじゃなかった気がしますが、でも「誰かに評価してもらえる」ことはとても嬉しくて、議論もさっぱりわからなくても、その場にいて意見を聞くだけでわくわくして、勉強になっていました。
なにより、ビジネスなんていうのは「自分の知らない世界」でした。これまでいた世界では議論されない内容、そして躍動感、初めて聞く「イノベーション」という言葉。そういうのに心が躍った記憶があります。自分の周りの人たちが、これまで誰一人してなかった「ビジネス」の世界の話をしている。高校生の頃、商売で知ってるのは「八百屋、電気屋」ぐらいだった自分が、そんな世界に身を置き始めました。そんなことしながら、3年間この組織で過ごしました。留年もしました。その間にたくさんのきっかけで、ベンチャーや研究組織でお世話になったりもしました。叱っていただいた社会人の方もいらっしゃいますし、ご迷惑をおかけした方もたくさんいます。何より、同期や後輩には迷惑をかけました。
その結果として、僕は「からっきし勉強(数学も)ができなくなった」わけですが、その代わりに社会や、ビジネスや、いろんな物事について議論できる仲間と巡り会いました。今、思えば、飛び込んで本当に良かった。学生組織であっても、人をマネージメントするということを経験できたし、人に伝えるというのはどういうことかを学んだし、企画をするときにまず何からするべきかを知りました。この経験は、どの場所にいっても活きています。
常識と非常識の境目で
逆に、この世界の常識は、別の世界では非常識なんだと思うことも増えてきます。自分の身の振り方1つを考えるのに、社会の動きは、他の人は、周りの反応は?といろんなことが気になるだけではなく、「どうしてみんなはそう考えるのか」ということに興味が出てきました。つまり、「考え方の形成過程」へ興味が出てきました。この頃から、ちょっとずつ普通の道からずれ始めます(笑。
それから、その当時僕が読んだ「イノベーションのジレンマ」という本、経営学の名著とも言われるクリステンセンの作品ですが、「過去に革新を起こした人」がどうして、「過去の成功にとらわれるのか」ということについて論じられる本ですが、これにもとても興味を惹かれました。
それから、当時は「起業家育成」の波が起こりはじめ、イベントが乱立し始めた時期だったと思います。2011年頃の話です(当時2回目の2年生)。その時、多くのイベントで「リスクを取らない人材」が多いとか、「起業家精神」とは何か、「チャレンジする」ことの重要性などが講演されていました。今でもされているかと思いますが。僕はこのとき思ったのですが「起業家精神」や「チャレンジする」ことの思考というのは「どうやって形成されるのか」「どうすれば後天的に形成できるか」に興味を持ち始めます。
それから、僕は「自己啓発」や「デザイン思考」などの思考・考え方に関する本を読むようになりました。ここまで見ても、随分と「右往左往」しながら進んでます。「U理論」のベースになっている本である「出現する未来」という本がありますが、これにはとても興味を惹かれました。そのあと「ダイアログ」「ワークショップ」などにも手を出して、色々と考えました。
ふとしたきっかけ
そんな僕が、大学4年生になった時、いきなり統計学を真剣に勉強し始めました。その理由は、「どうして自分は、何にでも熱中できるんだろう?」というふとした疑問からでした。その疑問に対して自分の中でも答えは「好きだったから(になったから)」だけではなく、「時間をたくさん使ったから」そして「打ち込んだ」からだと思ったんです。そこで、自分自身で実験を企ててみました。その実験は、次のようなものです。
まず、大学3年生の終了の段階で、おせじにも僕の数学と統計学の成績はそれほど芳しくはありませんでした。もちろん、数学に見向きもしなかった3年間と、3年生のときはワークショップに打ち込んでいましたからね笑(GPAも、ご想像よりかなり低いです。)。ただ、世間の流れは「データサイエンス」の方向に流れているし、この分野にいれば、将来への保証はある程度あるだろうという考えもありましたし、昔は数学得意だったんだぞという意味のわからない自信、そして何かおもしろいことできるだろう!という安易な思考によって背水の陣ではないということを確認した後で。。。
そんな僕が企てた実験は、「時間をたくさん使って、つらくても打ち込めば、何にでも熱中し、好きになるのか」ということでした。自分の人生の何年間かをかけた実験です(バカでしょ笑)。
これは、現在進行形で流れる実験です。でも、1年半たった今の段階で1つだけ言えることは「おそらく、自分の仮説は正しい」ということです。これは、僕だからなのか、それとも、みんなに共通することなのか確証を持って述べることはできませんが。少なくとも、僕は「統計学」を好きになったし、それ以上に「その周辺に興味を持ち、自分で楽しく探検する」ようになりました。
その要領で、大抵のことは「時間と根気」で好きになれるということがわかりました。この自信は、かなりかけがえのないもので、どんな場所でもある程度やっていけるという自信につながっていますし、「何だってやってみれば、好きになる」という感覚を持つことができるようになりました。
ちなみに、統計学について少し述べると、とにかく面白くて、なんでこんな現象があるのか、どうやって起こってるのかと思ったり、手法1つ見ても、すごいけどどこからこの発想を引っ張りだすのかと、触れていて本当に驚きと関心に満ちあふれた世界・学問だと思います。
ただ、統計学を始めたのは、こんな「よくわからない」理由からです。今、自分が立っている足場は外の方からは「統計学」ということになっていますが、僕にとっては「統計学」が軸にあるのではありません。むしろ、その背後には「ヒト」の思考、考え方の形成過程を明らかにしてみたいという想いがあります。それに、統計学は役に立つかと言われれば、結果的に役に立つものだったので良かったと思っています。データの解析はどんな場所でも必要のようですから。
まとめ
僕の大学生時代は、数学から始まり、ビジネスに移って、ベンチャー、イノベーション、起業家精神、ヒトと変わっていきました。そのせいか、今読む本も「哲学」と「脳科学」「遺伝子」などの方面に偏っています(もちろん「統計学」も読んでいますけど)。
ただ、とにかく、ヒトって疑問が尽きないです。とにかく面白くて、興味深くて。なんというか、わからないことだらけ。誰かに何かを言われた時、いつも「どうしてそう考えるのか?」という質問が僕の頭の中には浮かびますし、叱られてても、議論してても同じように「どうしてそう考えるのか」ということが気になって仕方ないです。
そして、その答えは、大抵はその人の経験や、生き方がとても深く関わっていて、そこから引き出されるストーリーにはとても大きな魅力がある。そして、それが、その人の思考の形成過程であり、僕が興味を惹かれる部分です。
なんか、書いてみたものの、とりとめのない話になってしまいました。
そのうち、最近興味のあるエピジェネティクスのわくわくする話を書こうと思います。
今日はこれぐらいにします。
ヒートマップで行列を可視化する! -ggplot2を用いたmicroarray発現量の可視化をしよう!-
今日のテーマは「ヒートマップ」
ヒートマップというのは、行列を可視化する時などに便利な手法です。有名なのは「遺伝子発現」というのを可視化する場合です。この他、店舗の一人の人が買った商品を可視化するのに使ってみてもおもしろいかもしれません。同じような購買パターンの人が視覚的にわかるようになります。一応、ヒートマップについてWeblioから引用しておきます。
ヒートマップ(英: Heat map)は個々の値のデータ行列を色として表現した可視化グラフの一種である。フラクタル図や樹形図は、変数によるヒエラルキー値を表現するため同様に色分ける事が多い。また、この用語は主題図の一種である階級区分図を示す。
用いるデータ
今回は、遺伝子発現データを用います。データは(ヒートマップ heatmap | R,マイクロアレイなどの遺伝子発現量の図示などによく使われる)で用いられているものをお借りしました。実際のデータを見ておくと、
> data <- read.table("http://stat.biopapyrus.net/data/arraydata.txt", header = TRUE)
> data <- as.matrix(data)
> head(data)
AF AX AC AT AN BF BX BC BT BN
gene1 -0.01183 1.37744 0.67014 0.82689 0.87908 0.88640 0.49236 0.88016 0.10693 0.38530
gene2 -0.00600 0.19820 -0.17458 -0.87388 0.19304 -0.13020 -1.56783 0.33063 -1.19051 -0.72618
gene3 -0.41678 0.52872 0.01384 0.08311 0.30768 -0.27890 0.48269 0.21181 0.37127 -0.32058
gene4 -0.69614 0.32774 -1.21520 -0.31868 -0.70187 -0.53080 -0.12315 -0.48518 -0.71129 -1.02066
gene5 0.91733 -1.23051 -0.32244 0.95149 -1.40095 -0.82365 -1.56783 -0.89023 -0.48405 -1.39034
gene6 1.46852 1.81342 3.12429 3.60012 1.93483 2.08088 1.63321 3.06953 2.32866 2.04482さて、このデータをぱっと見ても、数値が並んでいるだけでわかりません。このデータの数値を可視化したいという課題に今回はアタックします。それがヒートマップです。実際、データ引用元でも普通にヒートマップをggplot2を使わないでもかけるよとあるんですが、まぁggplot2でも書いてみたいので、書いてみましょう。
heatmap by ggplot2
ggplot2でヒートマップを書くのは、そんなに単純ではありません。普通のheatmap関数を用いるときは、ただデータを引数に取ればいいんですが、ggplot2では関数が使えるようにデータを加工する必要があります。その加工はreshape2のmelt関数を用いて、データを以下のように展開するという操作に対応します。
> #library# > library(ggplot2) > library(reshape2) > library(ggthemes) > > #data arrange# > data2=melt(data,id.var="AF") > head(data2) Var1 Var2 value 1 gene1 AF -0.01183 2 gene2 AF -0.00600 3 gene3 AF -0.41678 4 gene4 AF -0.69614 5 gene5 AF 0.91733 6 gene6 AF 1.46852
このように展開できたら、ggplot2を用いてヒートマップを書くことができます。ここで、heatmapを書くための関数としてgeom_tilesを用いています。X軸とY軸はggplotの中のaesで指定して、中の値を何で埋める(fill)かを選ぶわけですが、そのとき上でいうvalueの値で埋めますという意味です。最後のscale_fill_gradientはヒートマップの色の指定です。普通に書いてしまうと、ヒートマップは「濃い青〜薄い青」という非常にみえにくい感じになるので、小さい値には”white"、大きな値は"red"で塗りつぶして!というのが最後の意味です。
> #heatmap# > (p<-ggplot(data2,aes(as.factor(Var1),as.factor(Var2)))+geom_tile(aes(fill=value))+scale_fill_gradient(low="white",high="red"))
図を書いてみると、以下のようになります。

さて、しかしながら、X軸のラベルがみえにくいですよね。これを解消しましょう。それから、右側にある凡例も消してしまいましょう。余白も小さくして。そのためには以下のようにコマンドを書きます。
> #-heatmap-# > p + labs(x = "",y = "") + scale_x_discrete(expand = c(0, 0)) + scale_y_discrete(expand = c(0, 0)) + theme(legend.position = "none",axis.ticks = element_blank(), axis.text.x = element_text(size = 7, angle = 280, hjust = 0, colour = "grey50"))
ここで、余白の指定はscale_x_discrete(expand = c(0, 0)) + scale_y_discrete(expand = c(0, 0)) で行っています。これは余白を0にせよという意味です。次のthemeでlegend.position="none"と書いているのが凡例を消す操作。axis.ticks=element_blank()は軸を消す操作。axis.text.x = element_text(size = 7, angle = 280, hjust = 0, colour = "grey50"))でラベルに表示する文字の大きさ、その回転角などを指定しています。このようにして書くと、図は...

とそこそこ見やすくなりました。以上でggplot2でheatmapを書けたことになります。ただ、もうちょっとわかりやすくしたいんですけどね。実際にRに入ってるheatmap関数を使った図を見てみると、あー、こっちの方がいいなと思います。
heatmap関数によるヒートマップ作成
以下のようにコマンドを打ちます。すると、ヒートマップが作成されます。簡単です。しかも、クラスタリングした結果まで書くことができます。これggplot2で書こうと思うときっと大変なんだと思います...
> heatmap( + data, # 行列型データ + main = "Heat colors", # グラフタイトル + Rowv = TRUE, # 列にクラスタ図を描く + Colv = TRUE, # 行にクラスタ図を描かない + distfun = dist, # distance calculation + hclustfun = hclust, # clustering method + col = heat.colors(256), # 色彩の指定 + )

まとめ
今回は、ヒートマップを用いてデータを可視化してみました。最初にもいいましたが、これでマーケティングデータを可視化することができれば、ユーザーが共通して買っているものや、この人は買っているけど、この人は買っていないなどわかりそうですね。ちなみに、エクセルでもこれはできるようです...やる気にはなりませんけどwww
追記...こんなこともできます。
ヒートマップの中に値を書き込みたいなという場合には、次のようにすることで図を書くことができます。ただし、行・列数が多い場合にはきつそうです。。。
> dat <- matrix(rnorm(100, 3, 1), ncol=10)
> names(dat) <- paste("X", 1:10)
> dat2 <- melt(dat, id.var = "X1")
> ggplot(dat2, aes(as.factor(Var1), Var2, group=Var2)) +
+ geom_tile(aes(fill = value)) +
+ geom_text(aes(fill = dat2$value, label = round(dat2$value, 1))) +
+ scale_fill_gradient(low = "white", high = "red") 
オープンデータを解析する- ggplot2を用いたボロノイ分割で厚木市のコンビニ出店を見てみよう!-
オープンデータ
今日もオープンデータを可視化して、何かの役に立ててみようということをやってみたいと思います。昔、同級生が卒業研究で画像認識をやっていて、そのときに「ボロノイ分割」というものがありました。聞いているとですね、いろんな分野に応用されている手法で下のようなものに実際使われているようです。
で、今回はこのボロノイ分割を使って、厚木市の「コンビニ」の所在地を可視化してみようと思います。なぜ厚木市かというと、コンビニのデータが公開されているのって、厚木市しかなくて...どこかに落ちてるところがあれば教えてください。
ボロノイ分割とは
ボロノイ分割については、ボロノイ図とはを見ていただくとわかりやすいと思いますが、簡単にいえば、「平面上に、いくつかの点が配置されているとき、その平面上の点を、どの点に最も近いかによって分割してできる図」のことです。イメージがわかりにくいので、下の図を見ていただければ何となくわかってもらえるかと。

今回は、この真ん中の「母点」がコンビニの位置です。で、求めたいのは「ボロノイ境界」ということになります。
データの中身
解析なので、まずはデータから確認します。今回用いたデータはここのページ(厚木市コンビニデータ|Open data sharing & Download|LinkData)から落とすことのできる「コンビニデータ」です。このデータを用いて解析を行います。
> head(df) id 住所 緯度 経度 店舗の種類 お店の店名 連絡先 1 神奈川県厚木市三田南2丁目21番9号 35.47149 139.3483 セブン-イレブン セブンイレブン三田店 046-242-1171 2 神奈川県厚木市妻田南1丁目17−25 35.45299 139.3600 セブン-イレブン セブンイレブン妻田南店 046-223-8455 3 神奈川県厚木市下荻野1049−1 35.48385 139.3415 セブン-イレブン セブンイレブン厚木下荻野店 046-241-5830 4 神奈川県厚木市金田119−1 35.47002 139.3683 セブン-イレブン セブンイレブン厚木金田店 046-225-5572 5 神奈川県厚木市妻田東3丁目2−7 35.45966 139.3597 セブン-イレブン セブンイレブン厚木妻田店 046-221-0676 6 神奈川県厚木市七沢238 35.44230 139.2991 セブン-イレブン セブンイレブン厚木七沢店 046-248-0531
必要なのは、データの中で「店舗の種類」と「緯度」と「経度」ですから、これらをstore, lat, lonという変数にした次のようなデータフレームを用います。
> head(df)
lat lon store
1 35.47149 139.3483 セブン-イレブン
2 35.45299 139.3600 セブン-イレブン
3 35.48385 139.3415 セブン-イレブン
4 35.47002 139.3683 セブン-イレブン
5 35.45966 139.3597 セブン-イレブン
6 35.44230 139.2991 セブン-イレブン
ボロノイ図を書くために...
さて、ここからは具体的な解析を行っていきますが、いろんなパッケージを使います。
- ggplot2 : 図を書くために使います
- deldir:ボロノイ分割を行うパッケージ
- reshape2:データをggplot2用に変換するのに使います。
- plyr:データの分割・処理・結合 -> 「plyrパッケージで君も前処理スタ☆」改め「plyrパッケージ徹底入門」
- ggmap:地図を書くためのパッケージ
結構、いろんなものに依存しているのでややこしいですがご了承ください。
setwd("~/Desktop/blog/厚木_コンビニ")
library(ggplot2)
library(deldir)
library(reshape2)
library(plyr)
library(ggmap)
#data.frame
df = read.csv("data_conv.csv",sep="\t",header=F)
df = df[,c(3,4,5)]
names(df) = c("lat","lon","store")
#日本語フォントを使えるようにする
quartzFonts(maru=quartzFont(rep("HiraMaruProN-W4",4)),kaku =quartzFont(rep("HiraKakuPro-W6",4)))
#map
#地図の範囲
loc=c(min(df$lon),min(df$lat),max(df$lon),max(df$lat))
#googleから地図データを取得(zoomの大きさを間違えるとこの後エラーがでます。ggplotするところで missing valueとか, 今回は12 or 13)
M=ggmap(get_map(location=loc,zoom=12,source="google"))+xlab("")+ylab("")ここまでで、実は特定の区域を書くことができました。この辺りの流れについては、オープンデータを使ってみよう!-流山市の桜を最適なルートで回ろう!- - Data Science by R and Pythonを参照していただければわかりやすいかと。ここからは、本格的にボロノイ分割を行います。そのためには、まず、先ほど作成したデータフレームdfから、緯度と経度を取ってこないといけません。
############################# #data.frame only lat and lon# ############################# dd <- df[,1:2]
次にhullというものを考えましょう。hullというのは「(果物などの)外皮」のことですが、今回は、データの点集合の一番外側の点ということです。具体的には得られた図を見ていただくのが良いかと思います。
############# #convex hull# ############# hull = chull(dd) hullPointsIndices <- c(hull, hull[1]) #最後に1点加えているのは、点を回って戻ってくる直線を描くため, 下のqplotで意味が分かる。 hullPoly_df <- df[hullPointsIndices,] #上で指定した行だけ抜き出し # plot convex hull qplot(lon, lat, data = dd) + geom_polygon(data = hullPoly_df, colour = 'red', fill = 'red',alpha = I(1/10), size = 1)

外側の点だけ取ってプロットしました。つまり、この範囲にすべての点が入っていることになります。これは何かに使うわけではないですが、図示するときなどには、外枠がある方が見やすいので書いてみました。
次に、ボロノイ分割の計算です。ここで、ボロノイ分割の計算にはdeldirという関数を用いています。その前にrange, expand.rangeという関数を用いていますが、これはコードの中の説明を見てください。簡単にいえば、ボロノイ分割のデータの範囲を絞るために行っています(deldirのrw指定箇所)。
############# #triangulate# ############# #range::データの最大値と最小値を返す #expand_range(x,y):xのうち小さいもののy倍をz=xyとすると、x-z, y+zを計算する #図を書く範囲を限るために計算する xrng <- expand_range(range(dd$lon), .05) yrng <- expand_range(range(dd$lat), .05) #deldir::分割 deldir <- deldir(x=dd$lon,y=dd$lat, rw = c(xrng, yrng))
さて、deldirが返してくる結果には様々なリストが入っています。詳しくは以下のURLから参照していただきたいですが、先ほどの図でいえば、ボロノイ境界のデータが入っています。この他、以下の図(これも先ほどのHPより引用)でいえば、ドロネー図の情報も入っています。

http://cran.r-project.org/web/packages/deldir/deldir.pdf
さて、ドロネー図というものを書いてみましょう。
#################
#Delaunay fugure#
#################
qplot(lon, lat, data = dd) + geom_segment(aes(x = x1, y = y1, xend = x2, yend = y2), size = .5,data = deldir$delsgs, colour = 'red', alpha = .5)
############################
# triangulate with polygons#
############################
trilist <- unclass(triang.list(deldir)) #クラス構造を分解します
tridf <- melt(trilist, id.vars = c('x','y'))[,c(3,1:2)] #ggplot用に加工します, meltは便利!
names(tridf) <- c('tri','x','y')
qplot(lon, lat, data = dd) + geom_polygon(aes(x=x, y=y, fill=factor(tri)), data = tridf, colour = 'black', alpha = .5) + scale_fill_discrete(guide = FALSE)そのドロネー図がこちらになります。この図が、何の役に立つのかは後ほどわかります。

次に、この図に色を付けてみます。これも、何の意味があるかは後ほどです。

さて、ここで使っているgeom_polygonという関数が、空間を色で塗りつぶすための関数です。これを使うとボロノイ図が奇麗に書けます。その、ボロノイ図を次に書いていきましょう。ボロノイ図を書くためのデータも先ほどdeldirで作成したデータの中に入っています。上のものと同じようにして、以下のコマンドを打ってやれば...(今回は後ろ側に地図を入れます!)
######### #voronoi# ######### #分割図のみを作成する(色をぬったりしない) M + geom_point(aes(x=lon, y=lat,colour=factor(store)),size=3, data = df) + geom_segment(aes(x = x1, y = y1, xend = x2, yend = y2), size = .25,data = deldir$dirsgs, linetype = 2)
図は、こんな感じになります

このままじゃ寂しいので、領域に色をぬりましょう!ということをするためには、geom_polygonです。書いてみると、次のようになります。
#######################
#voronoi with polygons#
#######################
tilelist <- unclass(tile.list(deldir))
tilelist <- lapply(tilelist, function(l){
data.frame(x = l$x, y = l$y)
})
#melt(tilelist,id.var=c("x","y"))がうまくいかないので....
tiledf <- melt(tilelist, id.vars = c("x"))
tiledf <- tiledf[,c(4,1,3)]
names(tiledf) <- c('tile','x','y')
M + geom_polygon(aes(x = x, y = y, fill = factor(tile)),data = tiledf, colour = 'black', alpha = .3) + geom_point(aes(x = lon, y = lat,colour=factor(store)),size=2, data = df)+theme_set(theme_bw(base_size = 12,base_family="HiraMaruProN-W4"))結構奇麗に書けます。ただ問題がありまして...解消できてないんですけど、領域の色をコンビニの種類で分けたいんですが、どうもgeom_polygonでは無理かもしれなくて...解消法がわかる方教えていただけると嬉しいです。

図からわかりそうなこと。
先ほどお見せしたこの図に戻ってみましょう。すると、すぐわかることとしてコンビニが「どういうところ」に出店しているのかを傾向として見ることができます。図示の力といえますね。具体的には、こんなことが読み取れるんじゃないでしょうか?

まとめ
今回は、ボロノイ分割を用いてコンビニの出店傾向を探ってみました。図示ってやはり強力な手段です。何かの「仮説」を得る場合に、頭の中で想像するだけではなくて、「図示」することは非常に強力な手段になります。
罪滅ぼしのために奇麗に作った図とか...(苦笑)
M + geom_polygon(aes(x = x, y = y, fill = factor(tile)),data = tiledf, alpha = .5) + geom_segment(aes(x = x1, y = y1, xend = x2, yend = y2), size = .25,data = deldir$delsgs) + geom_segment(aes(x = x1, y = y1, xend = x2, yend = y2), size = .25,data = deldir$dirsgs, linetype = 2) + geom_polygon(data = hullPoly_df, colour = 'red', fill = NA,alpha = I(1/10), size = 2) + geom_point(aes(x=lon, y=lat), data = df,size = 5.75, alpha = .75) + geom_text(aes(x=lon,y=lat,label = 1:nrow(df)),data=df, size = 3, colour = 'green') + scale_fill_discrete(guide = FALSE)

線形モデルを簡単にわかりやすく! -データに直線を引いて、傾向を捉えるときの注意点-
線形モデルとは
今日のテーマは「線形モデル」です。多くの人が聞き慣れている「線形モデル」という言葉ですが、これについて今回はお話ししたいと思います。線形モデルは、他に「回帰モデル」という人もいますし、「線形回帰モデル」ということもあります。この辺の区別は、本来正確を期すべきですが、今回はここは気にしないで「線形モデル」を理解してもらうことに主眼を置きます。
線形モデルというのは、非常に単純なモデルです。下の図を見てください。データの点々によく当てはまる「線」を引いています。これはエクセルでも、統計ソフトでもなんでもできます。こうすると、実際にデータの傾向が見える化され、データから情報を引き出しやすくなります。今回は、この線形モデルの基本的なこと・それから注意点についてお話をします。少し統計的な言及を行いますが、できる限り直感的に説明をします。

用いるデータ
線形モデルを説明するために、今回は「データ」を用いることにします。ここでは、仮想のデータですが「農地に投入した肥料(変数名:fert)」と「収穫量(変数名:harvast)」の関係性を考えていきます。ここで、回帰モデルを考える時は「説明したい変数, 説明される変数, 予測したい変数」のことを「目的変数」と呼びます。つまり「収穫量」が目的変数です。一方で、「予測したい変数」を「説明する変数」今回であれば「農地に投入する肥料の量」を説明変数と呼びます。これは覚えてください。以下がデータです。ここで、最後の列の変数名「harvest_log」は「収穫量を対数変換」したものです。
> head(dat) #データの最初の行だけ見ます fert harvest harvest_log 1 15 68.47501 4.226469 2 12 32.80894 3.490701 3 27 134.21358 4.899432 4 2 149.71490 5.008733 5 23 34.95415 3.554037 6 24 183.13655 5.210232
やりたいこと
さて、行いたいことは「肥料の量」と「収穫量」には「どのような関係性」があるのかを確かめるということだとします。すると、真っ先に思いつくのは、横軸に、「肥料の量」をとり、縦軸に「収穫量」を取るようなことです。実際に図にしてみると、次のようになります。

この図から、読み取れることとしては、「肥料の量」が多くなるに連れて、「収穫量」は「指数的に」増えていることが見て取れます。つまり、式として書けば...
となっています。
線形モデルとは
さて、ここで、「線形モデル」の「線形」の意味を考えておくと、「線形」というのは、「目的変数」と「説明変数」の関係性が線形ですということを意味しています。これはどういうことかというと、目的変数は次のように表されますという仮定を置いています。言葉にすれば次のようになります。
数式では...(正確には、今回のケースでYやXはベクトルです)
これを見ればわかっていただけるように「線形モデル」の「線形」の意味は「目的変数」と「説明変数」の関係性の間に「非線形な関係」が紛れ込んではいけないのです。例えば「exp」とか「log」とかの関係性が入ると、途端に仮定が崩れて「線形モデル」を使うことはできません。ただし、モデルへ取り込む方法はありますが、それは次のエントリーで書くことにします。ただ、YとXの関係が"Y=exp(X)*b+e"だと推測されるのに、"Y = Xb+e"とモデルを仮定してはいけませんという話です。
そのため、線形モデルを用いる際には「変数間」の関係性に注意する必要があります。想い出してほしいのですが「相関」についてのエントリー「相関係数」ってなんですか? -意味と利点と欠点をわかりやすく- - Data Science by R and Pythonでも説明しましたが「説明変数」と「目的変数」の間の「線形性」に注意を払う必要があります。これを気にしないで「えいや!」ってやってしまうとろくな結果がでません。
実際に、線形回帰モデルの「回帰係数」上でいえば、にあたる部分の値というのは、目的変数Yと
の相関係数の関数なので、この値に依存しています。この点には注意してください。
今回のケース
そのため、今回のケースに線形回帰モデルを当てはめてはいけません。実際に当てはめてみると、次のような結果が得られます。図で確認しましょう。

これを見ていただくとわかるように、図から「外れている」ものがたくさんあります。特に「肥料の量」が大きくなると、「外れるのが大きく」なることが見て取れます。実は、このようなデータをそのまま扱う手段というのがあります。それは「Gamma分布を事前分布に仮定する」という方法で、一般化線形モデルの枠組みで話すことができます。でも、今回は「線形モデル」で扱うことに主眼があるので、このような場合の対処法を考えていきましょう。
指数的な関係性・対数的な関係性。
さて、目的変数と説明変数の間に、指数的な関係性があることがわかっています。指数的な関係というのは、具体的な例をだせば「xが1から2に増えると、Yはexp(1)=2.7 からexp(2)=7.4に増える」という関係性があるような状態です。今回のデータでは次のような関係です。
そんなときに効果的な対処の方法があります。それは両辺の「対数」を取るということです。両辺の対数を取ると、式は次のように変形されます。
これを見ていただくとわかる通り、これは、目的変数をlog(収穫量) とすれば、目的変数は「肥料の量」の線形式で表されるということを意味します。つまり、こうすれば「線形回帰」できるのです。実際に横軸は(肥料の量)で、縦軸をlog(収穫量) として図を書いてみます。すると、、、

このようなデータを得ることができました。このデータを見ていただくとわかるように、目的変数と説明変数の間には確かに「線形の関係」が存在することがわかります。これに回帰直線を引いたら次のような図が得られます。

奇麗に回帰ができているようにみえますね。
ネタばらし。
今回の架空のデータの生成方法についてここで書いておきますと、実は、モデルの片々を対数をとったら線形モデルになるようにデータを設計していました。コマンドは下に書いています。
このようにしているため、きちんとlogを取らないと正確な結果は得られません。実際に対数をとったものと、取ってないものを比較してみると以下のようになります。もちろんスケール変更しているため直接比較は難しいですが、対数を取ったケースを見ていただくと、切片を3.97532(本来は4)、fertの回帰係数の推定値0.02925(真の値は0.03)とうまく推定できていることがわかります。図を確認してから回帰する理由が何となくわかっていただけましたか?
#対数を取っていない場合
> glm(harvest ~ fert, data=dat)
Call: glm(formula = harvest ~ fert, data = dat)
Coefficients:
(Intercept) fert
37.935 3.889
Degrees of Freedom: 99 Total (i.e. Null); 98 Residual
Null Deviance: 874200
Residual Deviance: 615900 AIC: 1162
#対数を取った場合
> glm(harvest_log ~ fert, data=dat)
Call: glm(formula = harvest_log ~ fert, data = dat)
Coefficients:
(Intercept) fert
3.97532 0.02925
Degrees of Freedom: 99 Total (i.e. Null); 98 Residual
Null Deviance: 39.73
Residual Deviance: 25.12 AIC: 151.6
線形回帰モデルにおける重要な仮定
さて、線形回帰モデルにおけるもう1つ重要な仮定があります。これは、普通に「最小自乗法」という当てはめで線形回帰モデルが成り立ってるんだ!と思っていると、全く気づきませんが、知っておいてほしいことです。理由を説明し始めると、かなり長くなるので今回は紹介にとどめますが「等分散性」の仮定というものがあります。これは、なにかというと次の図を見てください。
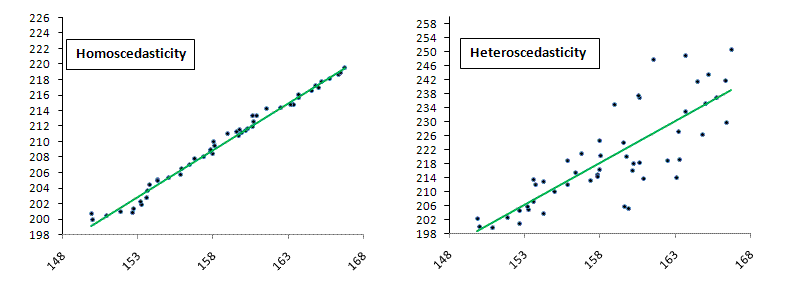
左側と右側の違いわかりますか?左側の方はX軸の値が大きくなっても、データのちらばりは変わりません。しかしながら、右の図を見ていただくと、X軸の値が大きくなるに連れて、データの散らばりが大きくなっています。
このような場合、左側は「等分散」であり、右側は「不均一分散」であると言います。そして、線形モデルには、データが「等分散である」という仮定が置かれていますので、目的変数と説明変数が「不均一分散」な関係性を持っている場合には「線形回帰モデル」は使うことができないというのが覚えておいて欲しいことです。
このような場合には、先ほど少しでてきた「一般化線形モデル」を用いたり、この他「線形混合モデル」、または「一般化線形混合モデル」さらには「一般化加法モデル」を用いたりします。このように、様々な手法を用いてこの問題を解消することができますが、線形モデルのみの枠組みでこの問題を取り扱うのはいささか難しいと言えます。
まとめ
さて、今回は「線形回帰モデル」について説明をしました。少し統計的な話も入ってきて、難しかった人もいるかもしれませんが、データ解析の基本が「図を書いて」「変数同士の関係性」をチェックするというところに変わりはありません。統計やデータの分析を行う際には、「図を書く」ことをとにかく大切にしてほしいと思います。
それから、線形回帰モデルというのは、今私たちが統計の世界で用いている手法の「基礎」になっているモデルです。実際、このモデルを拡張することで、様々なモデルが歴史的に作られてきました。なので、統計をやるにあたって「線形回帰モデル」をきちんと勉強して、使えるようになることは、ある意味その他の分野・手法を勉強・研究する際の大きな助けになります。是非、統計を始めよう!解析を始めようと思っている方は、「線形回帰モデル」からはじめてください!
お知らせ:データフェスト
データフェストを開催しますと以前ブログで書きましたが、開催の予定日程が変更になっていますのでご注意いただければと思います。会場の都合などで変更になりました、、、申し訳ないです。
【予告】データフェストを開催します!(仮) - Data Science by R and Python
コマンド
#wd
setwd("~/Desktop/blog/lm")
#library
library(ggplot2)
set.seed(100)
############
##dataの作成#
############
#肥料
fert=floor(runif(100,0,50))
#対数を取った収穫量
harvest_log=4+fert*0.03+rnorm(length(K),0,0.5)
#収穫量の観測値
harvest=exp(harvest_log)
#data
dat=data.frame(fert,harvest,harvest_log)
#plot by ggplot2
#lm not good
ggplot(data=dat,aes(x=fert,y=harvest))+geom_point()+xlab("amount of fertilizer")+ylab("harvest")
#lm not good
ggplot(data=dat,aes(x=fert,y=harvest))+geom_point()+geom_smooth(method="lm")+xlab("amount of fertilizer")+ylab("harvest")
#lm good
ggplot(data=dat,aes(x=fert,y=harvest_log))+geom_point()+xlab("amount of fertilizer")+ylab("log harvest")
#lm good
ggplot(data=dat,aes(x=fert,y=harvest_log))+geom_point()+geom_smooth(method="lm")+xlab("amount of fertilizer")+ylab("log harvest")
#glm result not good
glm(harvest ~ fert, data=dat)
#glm result good
glm(harvest_log ~ fert, data=dat)
大学のゼミどんなことしてるんですか? -数理科学・統計の中身-
雑記
久々に、実家に帰ってきまして。。。和歌山の海の近くでのんびりしながら、ブログを書いております。今日は、完全に雑記です。さて、大学で、研究室に所属すると「ゼミ」というものがあります。ゼミは、研究室毎にやり方が違います。基本は「研究の発表」や「相談」をする場所ですが、この場所がどういう機能を持っているのかいくつか最近実感することがあったので書いてみようかなと。
※ちなみに、理工系で大学3年生で研究室選びをしている人は、ゼミを見てから研究室を選ぶことをお勧めします。
所属している「数理科学科」について
まず、僕の所属している専攻・専修(分野・専攻)を書いておくと、「理工学専攻」の「数理科学専修」です。なので、基本的に「数学」の研究室だと思って読んでください。研究していることは「統計学」ですが、主に「数理的な」アプローチを大事にしています。極限、積分、確率論なども結構ガチでやることになります。これは、そんな数理科学を専攻する人が書いています。
ゼミ
数理科学をやっている人のゼミはどんな感じかというと、、、
- 基本的に週1回、時間は60 ~ 90分
- 1週間で準備してきたことを、前で黒板・白板でプレゼンテーション
- 90分間、先生から質問+突っ込み
- 基本的に同期と先生でやるけど、おおよそ先生1名 + 学生2~3名(ぐらい)
- 黒板は、こんな感じ。

注) 数学専攻と統計専攻で進め方が違うかもしれません。
僕のゼミは...
基本的に、1週間でゼミの準備です。研究テーマに関連する論文の読み込み、数式の展開の証明、必要な定理があれば論文の検索・証明、わからないところの明確化を1週間で行います。任意で補足資料の作成などもします。ただ、1週間しか期間がないので、pptやkeynoteなどはを作ったりはしません。
ゼミ(メリット)
さて、そんな少々ハードな「ゼミ」ですけど、いろいろと1年半ぐらいやってきて思うことがあります。それは、週に1回黒板に数式を書きながらプレゼンテーションを行っていると、とにかく「説明する」ことがうまくなります。それから「質問」に対して冷静に対処することができるようになります。基本的に「質問攻め」に毎週されているわけなので、場慣れはします。
あと、90分の発表内容を1週間でまとめるのが難しいことも多々あります。そういうときのための「その場しのぎのスキル」も得ることができます(笑。もともと、その場しのぎには自信があったのですが、より鍛えられるという結果になりました。
あと、「数理系」のゼミの良いところは、とにかく研究室全体の「人の数が少ないこと」にあります。そのおかげで、これだけのゼミの回数が実現されています。それから、教授は大学にいることが多いため相談もしやすいですし、同期と
ゼミ(デメリット)
ただし、ゼミをすると「プレゼンテーション」がうまくなるかと言えば、これは間違いです。大きく「誤解」されがちなことがあって、「人前で発表する」ことを通して、「発表」がうまくなることはあっても「伝えること」に関してはぷらすあるふぁの努力が必要になるなと思いました。「ゼミ」では、聞いてくれる人は「関連分野」の人ばかりですから、ある程度専門用語が通じますけど、実際にその話を外のヒトにするときには、どう説明すればいいのかと四苦八苦することがよくあります(理解不足なのかもしれませんが)。「異分野融合」なんて言葉が一時期ささやかれました、それから「産学連携」もよくテーマにあがります。でも、「言語が違う」ということが、随分と大きな壁になるんじゃないかなとよく思います。
この他の分野のゼミとか
噂や、話でしかきいたことはありませんが、「ゼミ」は本当に分野・研究室によって様々で、僕が聞いたことのある形式だけでも、おそらく5種類ぐらいあります。。。
- 週1回研究室の誰かが発表するのがベース(個別ゼミはあまりない)
- ドクターの人の研究にジョインして、研究グループでゼミする系
- 個人で研究して、先生に毎週進捗のみ報告する系
- などなど
まとめ
という感じで、数理科学科のゼミの紹介をしてみました。ゼミってあんまり「公開」されたり、「公開しても」見に来てくれなかったりするので、何かの役に立てば良いなと思います。
ちなみに、、、合宿とかもある...
すっごい楽しいですよ。
